機器學習有監督學習、無監督學習、半監督學習、主動學習、強化學習這5種學習方式；而根據所學知識（或模型）結構不同，可以使用諸如神經網絡、決策樹、規則、貝葉斯網絡等方法去構建學習算法；深度學習目前可以說是一種基于神經網絡的學習方法。而目前人工智能這么火爆，很大程度上歸功于深度學習等機器學習算法的成功應用，如阿爾法狗、沃森、翻譯機、人臉識別、無人車等。本篇聊聊深度學習。

“學習”倆字，就足以讓人們感受到機器的智能水平了。再加上“深度”倆字，原力君感覺鉆進了無邊無際的宇宙世界而不能自拔。這兩句話，只是為了表明我對深度學習這個名字的態度：它太唬人了！

深度學習的目的，是要得到樣本數據中輸入輸出數據之間的關系。這個關系實際上是一個函數，在實際工程中常用“模型”倆字來表示這個函數。為什么？因為一般人不知道函數，函數是有數學定義的；而一般人也不知道模型，但是模型可以讓人聽上去似懂非懂；而對理工科的同志來說，“函數”倆字表達的更清楚一些。實際中，深度學習常用來學習如何根據采集的數據來識別某一個物體，那這個“函數”在一定程度上就表征了這個物體的特性，因此大家也就常常用“模型”倆字來描述深度學習得到的函數關系。模型，包含了兩層含義：一是說模型實際上是一個函數關系，二是說這個函數是用來表征物體特性的。

深度學習可以看作是一種更高級的函數擬合方法

仔細回想一下我們高中學過的線性回歸方程，假設我們得到了一組關于施化肥量和水稻產量的數據：

這組數據繪制成二維平面圖之后，是一系列的散點。但是，我們可以使用一條直線去擬合施化肥量和水稻產量之間的關系。通常來說，直線方程可以表示為y=ax+b。在本例中，y代指水稻產量，x代指施化肥量，而a和b兩個參數用來表征施化肥量和水稻產量之間的數學關系。

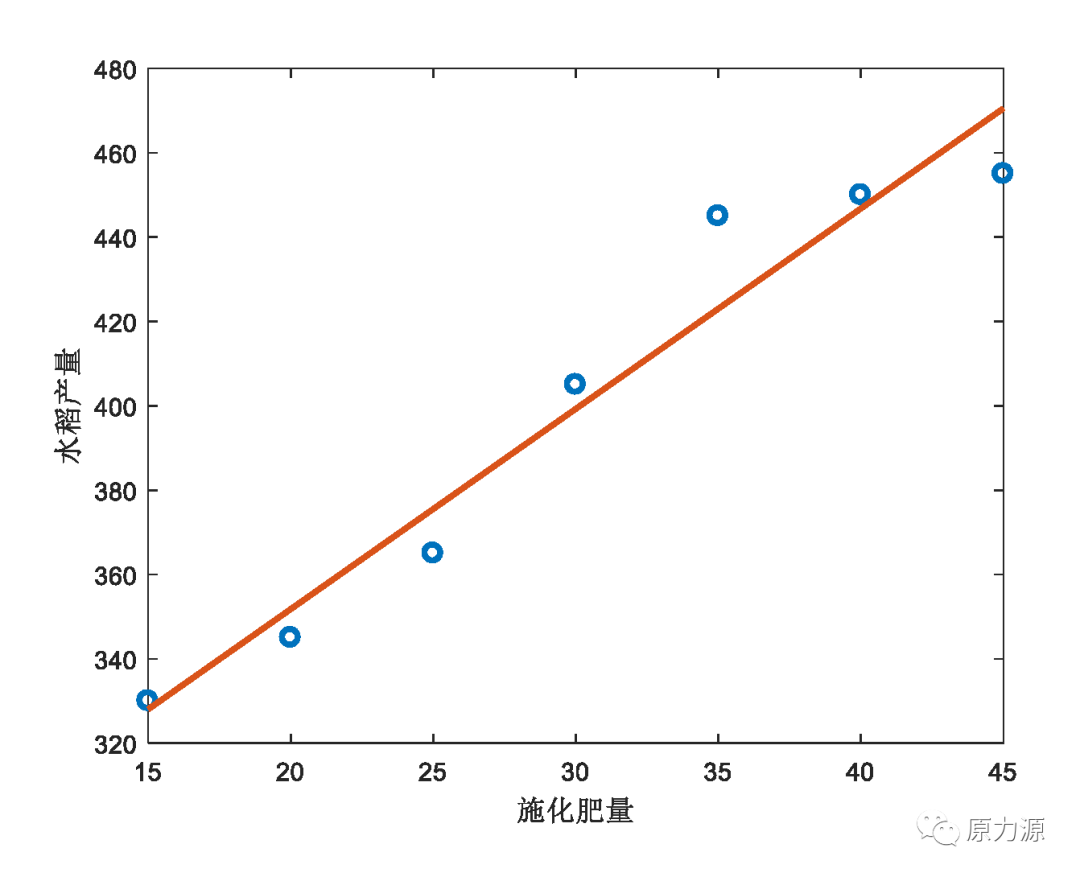
上面剛剛講到，深度學習最終的目的是得到一個模型來表征樣本數據所描述的系統，是不是感覺跟線性回歸問題很相似？

在實際工程中，我們的研究對象可能比較復雜，很難用一個線性方程來表示其模型。值得高興的是，研究者已經證明了一個事實：神經網絡可以用來表征任何形式的函數。因此，深度學習通常使用神經網絡來表征研究對象的模型。

有了神經網絡，深度學習要做的就是使用已有的樣本數據，利用合適的優化方法，去尋找能夠最好的描述研究對象特性的神經網絡參數。一旦得到了最優的參數，神經網絡就可以定型，我們就可以在實際應用中使用這個已定型的神經網絡來判斷采集的數據是否屬于我們的研究對象。當然，與線性回歸相比，深度學習的過程非常復雜。

人工神經網絡、激活函數、代價函數、梯度下降、反向傳播是深度學習的幾個關鍵點

人工神經網絡是深度學習的基礎，深度學習的結果通常是用神經網絡的形式表示的。與人的大腦神經網絡類似，人工神經網絡的基礎是人工神經元。單個神經元很簡單，但是非常多個神經元串聯并聯組合在一起之后，就會量變引起質變，生成一種復雜神經網絡。

激活函數是神經網絡中每個神經元的輸入輸出函數。為了利用深度學習得到最優神經網絡參數，激活函數必須是連續的。

代價函數是指給定輸入數據，神經網絡的輸出與樣本數據中真實的輸出數據偏差，通常用的是殘差平方和來表示，也有其他的表示方法，此處不表。

梯度下降法，是一種常見的原理比較簡單的優化求解算法。深度學習過程中，算法也是利用代價函數的變化來計算梯度（變化率，為正則變大，為負則變小）。我們的目的當然是讓代價函數越來越小，也就是讓其梯度一直為負，這就是梯度下降的意思。

反向傳播，可以看作是一種近似計算神經網絡代價函數對網絡參數梯度的方法。由于神經網絡結構的復雜性，我們沒法用一般的方法去計算其梯度，而反向傳播法提供了一種可行的方法。之所以叫反向傳播，是因為它采用了一種從網絡的最后一層開始計算梯度，逐步往前面一層推進，因此而得名。

神經網絡結構不同產生不同的深度學習方法

不同的神經網絡結構，會產生不用的深度學習方法，但是其基本思路大同小異。常見的神經網絡結構有：多層感知機、DNN深度神經網絡、CNN卷積神經網絡、RNN遞歸神經網絡等。但是不管使用什么樣的網絡結構，神經網絡最終是用來表征模型函數的，學習的過程都是通過微調參數觀察輸出來得到最優參數的。

一句話總結：深度學習可以看作是一種更高級的函數擬合方法；人工神經網絡、激活函數、代價函數、梯度下降、反向傳播是深度學習的幾個關鍵點；常見的深度學習神經網絡結構有多層感知機、DNN、CNN、RNN等。

聯系：highspeedlogic

QQ ：1224848052

微信：HuangL1121

郵箱：1224848052@qq.com

網站：http://www.mat7lab.com/

網站：http://www.hslogic.com/

微信掃一掃：